Kinematic Equation To Find Max Height

Kinematic Equation To Find Max Height. T (v_y=0) = v_y / g. The equations can be utilized for any motion that can be described as being either a constant velocity motion (an acceleration of 0 m/s/s) or a constant acceleration motion.

PPT Chapter 4, Motion in 2 Dimensions PowerPoint from www.slideserve.com

Using this we can rearrange the velocity equation to find the time it will take for the object to reach maximum height. (a) find the time when the ball reaches its maximum height. Y 3 = y 1 + v 1 δt + ½ a (δt) 2.

Source: cstephenmurray.com

Launching the object from the ground (initial height h = 0) horizontal velocity component: (a) find the time when the ball reaches its maximum height.

Source: fdocuments.in

So maximum height formula is: (a) v 0 = 125 m/s, θ = 37 degrees.

Source: www.pinterest.com

(a) v 0 = 125 m/s, θ = 37 degrees. T (v_y=0) = v_y / g.

Source: www.youtube.com

The maximum height is reached when v_y=0. Vx = v * cos(α) vertical velocity component:

Source: orvelleblog.blogspot.com

The maximum height is reached when v_y=0. We have motion with constant acceleration.

Source: www.slideserve.com

The equations can be utilized for any motion that can be described as being either a constant velocity motion (an acceleration of 0 m/s/s) or a constant acceleration motion. If v is the initial velocity, g = acceleration due to gravity and h = maximum height in meters, θ = angle of the initial velocity from the horizontal plane (radians or degrees).

Source: www.youtube.com

The maximum height of the water from the hose is 50.2 m. It means that the vertical velocity changes from positive to negative.

Source: www.slideserve.com

Check your understanding 4.3 a rock is thrown horizontally off a cliff 100.0 m 100.0 m high with a velocity of 15.0 m/s. For the maximum height, the formula is ymax = vy^2 / (2 * g) when using these equations, keep these points in mind:

Now, Find The Vertical Distance From The Surface At That Time:

V x (0) = v 0 cosθ = 99.8 m/s ~100 m/s, v y (0) = v 0 sinθ = 75.2 m/s ~ 75 m/s. While learning to fix kinematics problems, pupils generally have far too many equations bouncing around inside their heads. We can see that the most suitable kinematic equation to apply here is:

Using This We Can Rearrange The Velocity Equation To Find The Time It Will Take For The Object To Reach Maximum Height.

(a) v 0 = 125 m/s, θ = 37 degrees. \(h=\frac{u^2 \cdot \sin^2\theta}{2\cdot g} \) V = u + at.

For Example, The Final Velocity (V F) After Traveling To The Peak Would Be Assigned A Value Of 0 M/S.

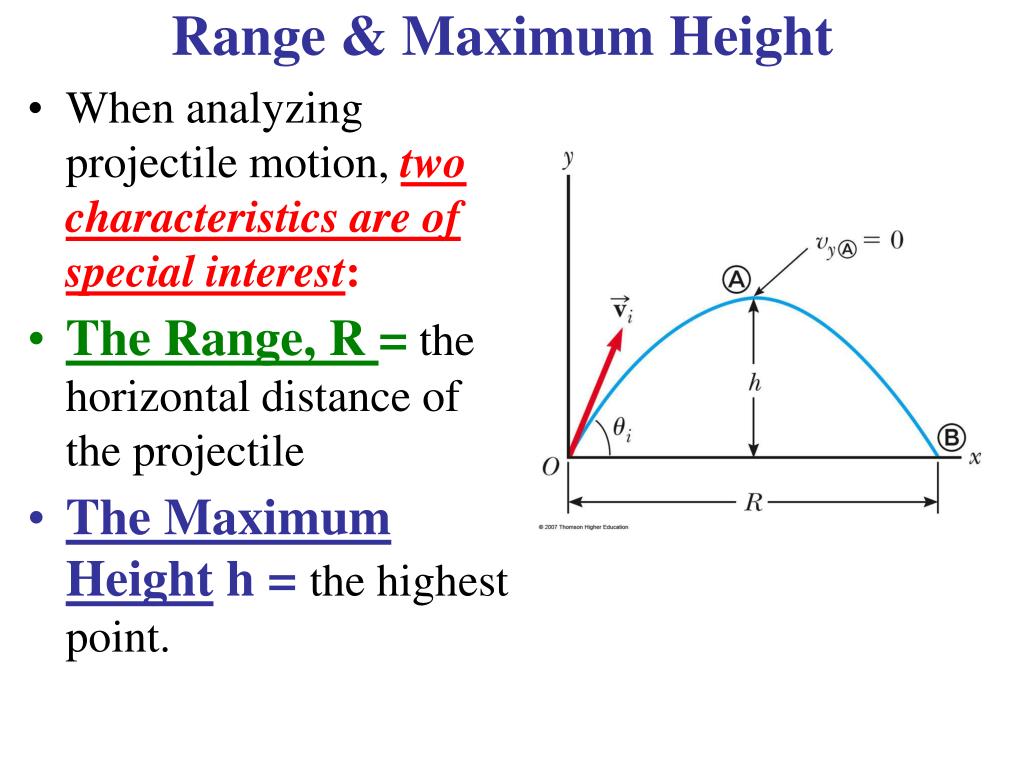
For the maximum height, the formula is ymax = vy^2 / (2 * g) when using these equations, keep these points in mind: The maximum height, y max, can be found from the equation: The maximum height is reached when v_y=0.

We Can Simplify By Combining The Terms To Get.

Write the velocity and position kinematic equations. Write the velocity and position kinematic equations: The speed of 6.4 m/s is about 14 mph, so is a reasonable answer.

This Equation Defines The Maximum Height Of A Projectile Above Its Launch Position And It Depends Only On The Vertical Component Of The Initial Velocity.

The maximum height of the water from the hose is 50.2 m. We have motion with constant acceleration. The maximum height of projectile is given by the formula: